In a given circuit diagram, a $5 \mathrm{~V}$ zener diode along with a series resistance is connected across a $50 \mathrm{~V}$ power supply. The minimum value of the resistance required, if the maximum zener current is $90 \mathrm{~mA}$ will be $\Omega$.
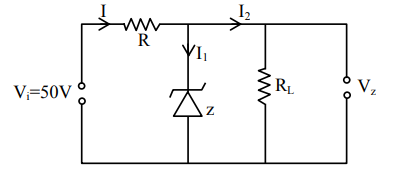
Voltage across $\mathrm{R}_{\mathrm{L}}=5 \mathrm{~V}$
$\Rightarrow \mathrm{i}_{2}=\frac{5}{\mathrm{R}_{\mathrm{L}}}$
Also voltage across $R=50-5=45$ volt
By $v=i R \Rightarrow R=\frac{v}{i}=\frac{45}{i_{i}+i_{2}}$
$\mathrm{R}=\frac{45}{90 \mathrm{~mA}+\frac{5}{\mathrm{R}_{\mathrm{L}}}}$
Current in zener diode is maximum when $\mathrm{R}_{\mathrm{L}} \rightarrow \infty$
$\left(\mathrm{i}_{2} \rightarrow 0\right.$ and $\left.\mathrm{i}_{\mathrm{i}}=\mathrm{i}\right)$
So $R=\frac{45}{90 m A}=500 \Omega$
