Question:
In a class of 60 students, 40 opted for $\mathrm{NCC}, 30$ opted for NSS and 20 opted for both NCC and NSS. If one of these students is selected at random, then the probability that the student selected has opted neither for NCC nor for NSS is :
Correct Option: , 2
Solution:
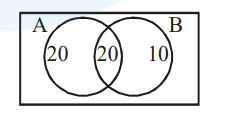
$\mathrm{A} \rightarrow$ opted NCC
$B \rightarrow$ opted NSS
$\therefore \mathrm{P}($ nither $\mathrm{A}$ nor $\mathrm{B})=\frac{10}{60}=\mathrm{z} \frac{1}{6}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.