In a circle of radius 14 cm, an arc subtends an angle of 120° at the centre.

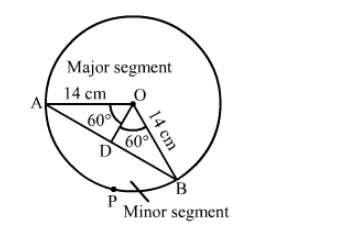
Radius of the circle, r = 14 cm
Draw a perpendicular OD to chord AB. It will bisect AB.
∠A = 180° − (90° + 60°) = 30°

$\cos 30^{\circ}=\frac{\mathrm{AD}}{\mathrm{OA}}$

$\Rightarrow \frac{\sqrt{3}}{2}=\frac{\mathrm{AD}}{14}$

$\Rightarrow \mathrm{AD}=7 \sqrt{3}$

$\Rightarrow \mathrm{AB}=2 \times \mathrm{AD}=14 \sqrt{3} \mathrm{~cm}$

$\sin 30^{\circ}=\frac{\mathrm{OD}}{\mathrm{OA}}$

$\Rightarrow \frac{1}{2}=\frac{\mathrm{OD}}{14}$

$\Rightarrow \mathrm{OD}=7 \mathrm{~cm}$

Area of minor segment = Area of sector OAPB − Area of triangle AOB

$=\frac{\theta}{360^{\circ}} \pi(\mathrm{OA})^{2}-\frac{1}{2} \times \mathrm{OD} \times \mathrm{AB}$

$=\frac{120^{\circ}}{360^{\circ}} \times \frac{22}{7}(14)^{2}-\frac{1}{2} \times 7 \times 14 \sqrt{3}$

$=205.33-84.77$

$=120.56 \mathrm{~cm}^{2}$

Hence, the correct answer is option (a).