In a ∆ABC right angled at B, ∠A = ∠C. Find the values of

(i) We have drawn the following figure related to given information

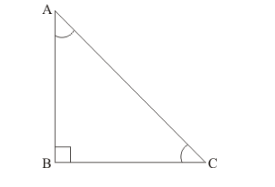
To find:

$\sin A \cos C+\cos A \sin C \ldots \ldots$ (1)

Now we have,

$\sin A=\frac{B C}{A C}, \sin A=\frac{A B}{A C}$

$\cos A=\frac{A B}{A C}, \cos C=\frac{B C}{A C}$

Now by substituting the above values in equation (1)

We get,

\sin A \cos C+\cos A \sin C=\frac{B C}{A C} \times \frac{B C}{A C}+\frac{A B}{A C} \times \frac{A B}{A C}

$=\frac{B C^{2}}{A C^{2}}+\frac{A B^{2}}{A C^{2}}$

$=\frac{B C^{2}+A B^{2}}{A C^{2}}$

Therefore,

$\sin A \cos C+\cos A \sin C=\frac{B C^{2}+A B^{2}}{A C^{2}}$.......(2)

Now in right angled $\triangle A B C$

By applying Pythagoras theorem

We get,

$A C^{2}=A B^{2}+B C^{2}$

Now, by substituting above value of $A C^{2}$ in equation (2)

We get,

$\sin A \cos C+\cos A \sin C=\frac{B C^{2}+A B^{2}}{A B^{2}+B C^{2}}$

$\Rightarrow \sin A \cos C+\cos A \sin C=\frac{A B^{2}+B C^{2}}{A B^{2}+B C^{2}}$

Now both numerator and denominator contains $A B^{2}+B C^{2}$

Therefore it gets cancelled and 1 remains

Hence $\sin A \cos C+\cos A \sin C=1$

(ii) We have drawn the following figure

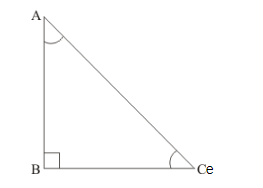
To find:

$\sin A \sin B+\cos A \cos B$....(1)

Now we know that sum of all the angles of any triangle is 180°

Therefore,

$\angle A+\angle B+\angle C=180^{\circ}$

Since $\angle A=\angle C$ and $\angle B=90^{\circ}$

Therefore,

$\angle A+90^{\circ}+\angle A=180^{\circ}$

$\Rightarrow 2 \angle A+90^{\circ}=180^{\circ}$

$\Rightarrow \quad 2 \angle A=180^{\circ}-90^{\circ}$

$\Rightarrow \quad 2 \angle A=90^{\circ}$

$\Rightarrow \quad \angle A=\frac{90^{\circ}}{2}$

$\Rightarrow \quad \angle A=45^{\circ}$

It is given that $\angle A=\angle C$

Therefore,

$\angle A=\angle C=45^{\circ} \ldots \ldots(2)$

Now we have,

$\sin A=\frac{B C}{A C}, \sin B=\sin 90^{\circ}=1$

$\cos A=\frac{A B}{A C}, \cos B=\cos 90^{\circ}=0$

Now by substituting the above values in equation (1)

We get,

$\sin A \sin B+\cos A \cos B=\sin 45^{\circ} \times 1+\cos 45^{\circ} \times 0$

$=\sin 45^{\circ}$

Since $\sin 45^{\circ}=\frac{1}{\sqrt{2}}$

Therefore $\sin A \sin B+\cos A \cos B=\frac{1}{\sqrt{2}}$