In a $\triangle A B C, \angle A=x^{\circ}, \angle B=3 x^{\circ}$ and $\angle C=y^{\circ}$. If $3 y-5 x=30$, prove that the triangle is right angled.
We have to prove that the triangle is right
Given $\angle A=x^{\circ}, \angle B=3 x^{\circ}$ and $\angle C=y^{\circ}$
Sum of three angles in triangle are $\angle A+\angle B+\angle c=180^{\circ}$
$\angle A+\angle B+\angle c=180^{\circ}$
$x+3 x+y=180$
$4 x+y=180 \cdots(i)$
By solving $4 x+y=180$ with $3 y-5 x=30$ we get,
$4 x+y=180$
$-5 x+3 y=30 \cdots(i i)$
Multiplying equation ![]() by 3 we get
by 3 we get
$12 x+3 y=540 \cdots($ iii $)$
Subtracting equation (ii) from (iii)
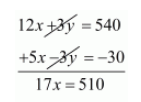
$x=\frac{510}{17}$
$x=30^{\circ}$
Substituting $x=30^{\circ}$ in equation $(i)$ we get
$4 x+y=180$
$4 \times 30+y=180$
$120+y=180$
$y=180-120$
$y=60^{\circ}$
Angles $\angle A, \angle B$ and $\angle C$ are
$\angle A=x^{\circ}$
$=30^{\circ}$
$\angle B=3 x^{\circ}$
$=3 \times 30^{\circ}$
$=90^{\circ}$
$\angle C=y^{\circ}$
$=60^{\circ}$
A right angled triangle is a triangle in which one side should has a right angle that is $90^{\circ}$ in it.
Hence, $\angle B=90^{\circ}$ The triangle $\mathrm{ABC}$ is right angled
