In a A A B C, D is the mid-point of side

Given In $\triangle A B C, D$ is the mid-point of $A C$ i.e., $A D=C D$ such that $B D=\frac{1}{2} A C$.

To show $\angle A B C=90^{\circ}$

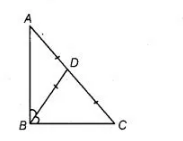
Proof We have,       $B D=\frac{1}{2} A C$     $\ldots(i)$

 Since, $D$ is the mid-point of $A C$.

$\therefore$ $A D=C D=\frac{1}{2} A C$... (ii)

From Eqs. (i) and (ii), 

$A D=C D=B D$

$\begin{array}{lll}\ln \triangle D A B_{1} & A D=B D & \text { [proved above] }\end{array}$

$\therefore$ $\angle A B D=\angle B A D$ ..(iii)

[angles opposite to equal sides are equal]

In $\triangle D B C$, $B D=C D$ [proved above]

$\therefore \quad \angle B C D=\angle C B D \quad \ldots$ (iv)

[angles opposite to equal sides are equal]

In $\triangle A B C, \quad \angle A B C+\angle B A C+\angle A C B=180^{\circ}$ [by angle sum property of a triangle]

$\Rightarrow \quad \angle A B C+\angle B A D+\angle D C B=180^{\circ}$

$\Rightarrow \quad \angle A B C+\angle A B D+\angle C B D=180^{\circ}$ [from Eqs.(iii) and (iv)]

$\Rightarrow \quad \angle A B C+\angle A B C=180^{\circ}$

$2 \angle A B C=180^{\circ}$

$\Rightarrow \quad \angle A B C=90^{\circ}$