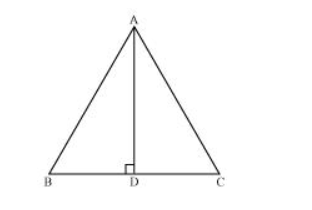
In ΔABC, AD is the perpendicular bisector of BC (see the given figure). Show that ΔABC is an isosceles triangle in which AB = AC.
Solution:
In $\triangle A D C$ and $\triangle A D B$,
$A D=A D$ (Common)
$\angle A D C=\angle A D B\left(\right.$ Each $\left.90^{\circ}\right)$
$C D=B D(A D$ is the perpendicular bisector of $B C)$
$\therefore \triangle \mathrm{ADC} \cong \triangle \mathrm{ADB}($ By $S A S$ congruence rule $)$
$\therefore \mathrm{AB}=\mathrm{AC}(\mathrm{By} \mathrm{CPCT})$
Therefore, $A B C$ is an isosceles triangle in which $A B=A C$.
