If zeros of the polynomial f(x) = x3 − 3px2 + qx − r are in A.P.,

Solution:

Let $a-d, a, a+d$ be the zeros of the polynomial $f(x)=x^{3}-3 p x^{2}+q x-r$ then

Sum of zeros $=\frac{-\text { Coefficient of } x^{2}}{\text { Coefficient of } x^{3}}$

$(a-d)+a+(a+d)=\frac{-(-3 p)}{1}$

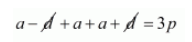
$3 a=3 p$

$a=\frac{3}{3} p$

$a=p$

Since $a$ is a zero of the polynomial $f(x)$

Therefore,

$f(a)=0$

$a^{3}-3 p a^{2}+q a-r=0$

Substituting $a=p$. we get

$p^{3}-3 p(p)^{2}+q \times p-r=0$

$p^{3}-3 p^{3}+q p-r=0$

$-2 p^{3}+q p-r=0$

$q p-r=2 p^{3}$

Hence, the correct choice is $(a)$