If two lines intersect prove that the vertically

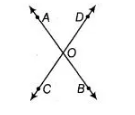
Given Two lines AB and CD intersect at point O.

To prove

(i) $\angle A O C=\angle B O D$

(ii)$\angle A O D=\angle B O C$

Proof

(i) Since, ray $O A$ stands on line $C D$.

$\therefore$ $\angle A O C+\angle A O D=180^{\circ}$ [linear pair axiom]...(1)

Since, ray $O D$ stands on line $A B$.

 $\therefore$ $\angle A O D+\angle B O D=180^{\circ}$ [linear pair axiom] ...(ii)

From Eqs. (i) and (ii).

$\angle A O C+\angle A O D=\angle A O D+\angle B O D$

$\Rightarrow$ $\angle A O C=\angle B O D$

(ii) Since, ray $O D$ stands on line $A B$.

$\therefore$ $\angle A O D+\angle B O D=180^{\circ}$ [linear pair axiom].....(iii)

Since, ray $O B$ stands on line $C D$.

$\therefore \quad \angle D O B+\angle B O C=180^{\circ}$ $\ldots(\mathrm{iv})$

From Eqs. (iii) and (iv),

$\angle A O D+\angle B O D=\angle D O B+\angle B O C$

$\Rightarrow$ $\angle A O D=\angle B O C$ Hence proved.