If two diameters of a circle lie along the lines

Solution:

The point of intersection of two diameters is the centre of the circle.

$\therefore$ point of intersection of two diameters $x-y=9$ and $x-2 y=7$ is $(11,2)$.

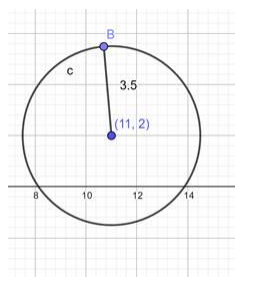
$\therefore$ centre $=(11,2)$

Area of a circle $=\pi r^{2}$

$38.5=\pi r^{2}$

$\Rightarrow r^{2}=\frac{38.5}{\pi}$

$\Rightarrow \mathrm{r}^{2}=12.25$ sq.cm

the equation of the circle is:

$(x-h)^{2}+(y-k)^{2}=r^{2}$

Where, (h, k) is the centre of the circle.

r is the radius of the circle.

$\Rightarrow(x-11)^{2}+(y-2)^{2}=12.25$

Ans: $(x-11)^{2}+(y-2)^{2}=12.25$