If two chords AB and CD of a circle

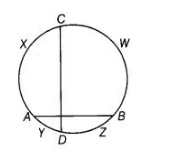
Given In a circle AYDZBWCX, two chords AB and CD intersect at right angles.

To prove arc CXA + arc DZB = arc AYD + arc BWC = Semi-circle.

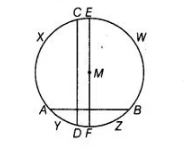
Construction Draw a diameter EF parallel to CD having centre M.

Proof Since, CD||EF

arc EC = arc PD … (i)

arc ECXA = arc EWB [symmetrical about diameter of a circle] arc AF = arc BF …(ii)

We know that,  $\operatorname{arc} E C X A Y D F=$ Semi-circle

$\operatorname{arc} E A+\operatorname{arc} A F=$ Semi-circle

$\Rightarrow \quad \operatorname{arc} E C+\operatorname{arcCXA}+\operatorname{arc} F B=$ Semi-circle $\quad$ [from Eq. (ii)]

$\Rightarrow \quad \operatorname{arc} D F+\operatorname{arc} C X A+\operatorname{arc} F B=$ Semi-circle $\quad$ [from Eq. (i)]

$\Rightarrow \quad \operatorname{arc} D F+\operatorname{arc} F B+\operatorname{arc} C X A=$ Semi-circle

$\Rightarrow \quad \operatorname{arc} D Z B+\operatorname{arc} C \times A=$ Semi-circle

We know that, circle divides itself in two semi-circles, therefore the remaining portion of the circle is also equal to the semi-ciccle.

$\therefore$ $\operatorname{arc} A Y D+\operatorname{arc} B W C=$ Semi-circle 

Hence proved.