If the variable line $3 x+4 y=\alpha$ lies between the two $\operatorname{circles}(x-1)^{2}+(y-1)^{2}=1$ and $(x-9)^{2}+(y-1)^{2}=4$ without intercepting a chord on either circle, then the sum of all the integral values of $\alpha$ is_______.
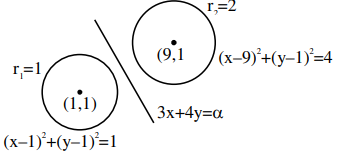
Both centres should lie on either side of the line as well as line can be tangent to circle.
$(3+4-\alpha) \cdot(27+4-\alpha)<0$
$(7-\alpha) \cdot(31-\alpha)<0 \Rightarrow \alpha \in(7,31) \ldots(1)$
$\mathrm{d}_{1}=$ distance of $(1,1)$ from line
$\mathrm{d}_{2}=$ distance of $(9,1)$ from line
$\mathrm{d}_{1} \geq \mathrm{r}_{1} \Rightarrow \frac{|7-\alpha|}{5} 1 \Rightarrow \alpha \in(-\infty, 2] \cup[12, \infty) \ldots(2)$
$\mathrm{d}_{2} \geq \mathrm{r}_{2} \Rightarrow \frac{|31-\alpha|}{5} \geq 2 \Rightarrow \alpha \in(-\infty, 21] \cup[41, \infty)$.....(3)
$(1) \cap(2) \cap(3) \Rightarrow \alpha \in[12,21]$
Sum of integers $=165$
