If the system of equations has infinitely many solutions, then

The given systems of equations are

$2 x+3 y=7$

$(a+b) x+(2 a-b) y=21$

For the equations to have infinite number of solutions, $\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}$

Here $a_{1}=2, a_{2}=(a+b), b_{1}=3, b_{2}=2 a-b, c_{1}=7, c_{2}=21$

$\frac{2}{a+b}=\frac{3}{2 a-b}=\frac{7}{21}$

Let us take $\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}$

$\frac{2}{a+b}=\frac{3}{2 a-b}$

By cross multiplication we get,

$2(2 a-b)=3(a+b)$

$4 a-2 b=3 a+3 b$

$4 a-3 a=3 b+2 b$

$a=5 b \cdots(i)$

Now take $\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}$

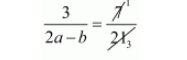
$\frac{3}{2 a-b}=\frac{1}{3}$

By cross multiplication we get,

$3 \times 3=1 \times 2 a-b$

$9=2 a-b \cdots(i i)$

Substitute $a=5 b$ in the above equation

$9=2 \times 5 b-b$

$9=10 b-b$

$9=9 b$

$\frac{9}{9}=b$

$1=b$

Substitute $b=1$ in equation $(i)$ we get, $a=5 b$

$a=5 \times 1$

$a=5$

Therefore $a=5$ and $b=1$.

Hence, the correct choice is $b$.