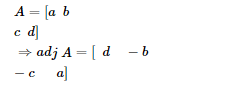Question:
If $S=\left[\begin{array}{ll}a & b \\ c & d\end{array}\right]$, then adj $A$ is
(a) $\left[\begin{array}{cc}-d & -b \\ -c & a\end{array}\right]$
(b) $\left[\begin{array}{cc}d & -b \\ -c & a\end{array}\right]$
(c) $\left[\begin{array}{ll}d & b \\ c & a\end{array}\right]$
(d) $\left[\begin{array}{ll}d & c \\ b & a\end{array}\right]$
Solution:
(b) $\left[\begin{array}{cc}d & -b \\ -c & a\end{array}\right]$
Adjoint of a square matrix of order 2 is obtained by interchanging the diagonal elements and changing the signs of off-diagonal elements.
Here,