Question:
If the product of zeros of the polynomial $f(x) a x^{3}-6 x^{2}+11 x-6$ is 4 , then $a=$
(a) $\frac{3}{2}$
(b) $-\frac{3}{2}$
(c) $\frac{2}{3}$
(d) $-\frac{2}{3}$
Solution:
Since $\alpha$ and $\beta$ are the zeros of quadratic polynomial $f(x)=a x^{3}-6 x^{2}+11 x-6$
$\alpha \beta=\frac{-\text { Constant term }}{\text { Coefficient of } x^{2}}$
So we have
$4=-\left(\frac{-6}{a}\right)$
$4=\frac{6}{a}$
$4 a=6$
$a=\frac{6}{4}$
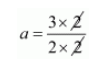
$a=\frac{3}{2}$
The value of $a$ is $\frac{3}{2}$
Hence, the correct alternative is $(a)$.
