Question:
If the perpendicular bisector of a chord $A B$ of a circle $P X A Q B Y$ intersects the circle at $P$ and $Q$, prove that arc $P X A=\operatorname{arc} P Y B$.
Thinking Process
Firstly, prove that $\triangle \mathrm{APM}$ is congruent to $\triangle \mathrm{BPM}$ by SAS rule, then further prove the required result by CPCT rule.
Solution:
Let $A B$ be a chord of a circle having centre at $O P Q$ be the perpendicular bisector of the chord $A B$, which intersects at $M$ and it always passes through $O$.
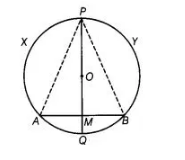
To prove arc PXA ≅ arc PYB
Construction Join AP and BP.
Proof In ΔAPM and ΔBPM,
AM = MB
∠PMA = ∠PMB
PM = PM
∴ ΔAPM s ΔBPM
∴PA = PB
=> arc PXA ≅ arc PYB
