Question:
If the minimum area of the triangle formed by a tangent to the ellipse $\frac{x^{2}}{b^{2}}+\frac{y^{2}}{4 a^{2}}=1$ and the co-ordinate axis is kab, then $\mathrm{k}$ is equal to
Solution:
Tangent
$\frac{x \cos \theta}{b}+\frac{y \sin \theta}{2 a}=1$
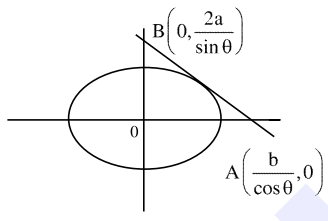
So, area $(\Delta \mathrm{OAB})=\frac{1}{2} \times \frac{\mathrm{b}}{\cos \theta} \times \frac{2 \mathrm{a}}{\sin \theta}$
$=\frac{2 a b}{\sin 2 \theta} \geq 2 a b$
$\Rightarrow k=2$
