Question:
If the length of the chord of the circle, $x^{2}+y^{2}=r^{2}(r>0)$ along the line, $y-2 x=3$ is $r$, then $r^{2}$ is equal to:
Correct Option: , 2
Solution:
In right $\triangle R S Q, \sin 60^{\circ}=\frac{R S}{r}$
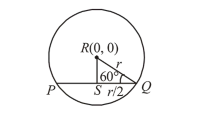
$\Rightarrow R S=r \times \frac{\sqrt{3}}{2}=\frac{\sqrt{3} r}{2}$
Now equation of $P Q$ is $y-2 x-3=0$
$\therefore \frac{\sqrt{3} r}{2}=\frac{|0+0-3|}{\sqrt{5}}$
$\Rightarrow \frac{\sqrt{3} r}{2}=\frac{3}{\sqrt{5}} \Rightarrow r=\frac{2 \sqrt{3}}{5} \Rightarrow r^{2}=\frac{12}{5}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.