If the heights of two right circular cones

Given that,

$h_{1}: h_{2}=1: 2$ and $2 \pi r_{1}: 2 \pi r_{2}=3: 4$

i.e., $r_{1}: r_{2}=3: 4$

Therefore,

The ratios of volume of their cones will be

$v_{1}: v_{2}=\frac{1}{3} \pi r_{1}^{2} h_{1}: \frac{1}{3} \pi r_{2}^{2} h_{2}$

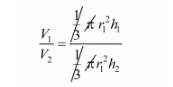
$=\left(\frac{r_{1}}{r_{2}}\right)^{1} \times\left(\frac{h_{1}}{h_{2}}\right)$

$\frac{V_{1}}{V_{2}}=\left(\frac{3}{4}\right)^{2} \times\left(\frac{1}{2}\right)$

$=\frac{9}{32}$

$V_{1}: V_{2}=9: 32$