Question:
If the function $\mathrm{f}: \mathrm{R}-\{1,-1\} \rightarrow \mathrm{A}$ defined by $\mathrm{f}(x)=\frac{x^{2}}{1-x^{2}}$, is
suriective, then $A$ is equal to:
Correct Option: , 3
Solution:
$f(x)=\frac{x^{2}}{1-x^{2}}$
$\Rightarrow f(-x)=\frac{x^{2}}{1-x^{2}}=f(x)$
$f^{\prime}(-x)=\frac{2 x}{\left(1-x^{2}\right)^{2}}$
$\therefore \mathrm{f}(\mathrm{x})$ increases in $\mathrm{x} \in(10, \infty)$
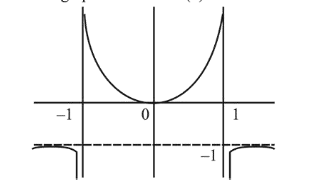
Also $\mathrm{f}(0)=0$ and
$\lim _{x \rightarrow \pm \infty} f(x)=-1$ and $\mathrm{f}(\mathrm{x})$ is even function
$\therefore \operatorname{Set} \mathrm{A}=\mathrm{R}-[-1,0)$
And the graph of function $f(x)$ is