If the equation 9x2 + 6kx + 4 = 0 has equal roots,

Solution:

The given quadric equation is $9 x^{2}+6 k x+4=0$, and roots are equal.

Then find roots of given equation.

Here, $a=9, b=6 k$ and,$c=4$

As we know that $D=b^{2}-4 a c$

Putting the value of $a=9, b=6 k$ and, $c=4$

$=(6 k)^{2}-4 \times 9 \times 4$

$=36 k^{2}-144$

The given equation will have equal roots, if $D=0$

$36 k^{2}-144=0$

$36\left(k^{2}-4\right)=0$

$k^{2}-4=0$

$k^{2}=4$

$k=\pm 2$

So, putting the value of k in quadratic equation

When $k=2$ then equation be and when $k=-2$ then

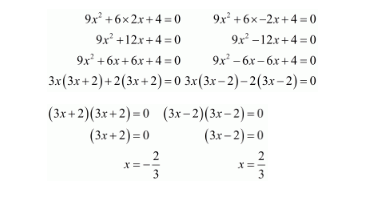
Therefore, the value of $x=\pm \frac{2}{3}$

Thus, the correct answer is (a)