If the bisector of the exterior vertical angle of a triangle be parallel to the base. Show that the triangle is isosceles.

Given that the bisector of the exterior vertical angle of a triangle is parallel to the base and we have to prove that the triangle is isosceles. Let ABC be a triangle such that AD is the angular bisector of exterior vertical angle EAC and

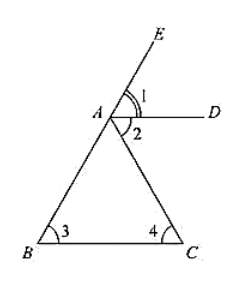
AD ∥ BC

Let ∠EAD = (i), ∠DAC = (ii), ∠ABC = (iii) and ∠ACB = (iv)

We have,

(i) = (ii)                       [AD is a bisector of ∠EAC]

(i) = (iii)                      [Corresponding angles]

and (ii) = (iv)             [alternative angle]

(iii) = (iv)

AB = AC

Since, in ΔABC, two sides AB and AC are equal we can say that ΔABC is isosceles triangle.