If the bisector of an angle of a triangle bisects the opposite side, then the triangle is

(c) isosceles

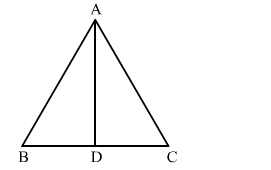
Let AD be the angle bisector of angle A in triangle ABC.
Applying angle bisector theorem, we get:

$\frac{A B}{A C}=\frac{B D}{D C}$

It is given that AD bisects BC.
Therefore, BD = DC

$\Rightarrow \frac{A B}{A C}=1$

$\Rightarrow A B=A C$

Therefore, the triangle is isosceles.