If the area of the bounded region

$R=\left\{(x, y): \max \left(0, \log _{e} x\right) \leq y \leq 2^{x}, \frac{1}{2} \leq x \leq 2\right\}$

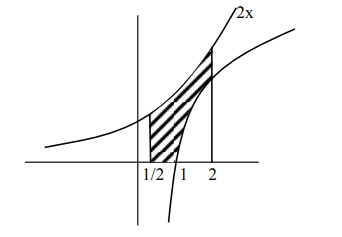
$\int_{\frac{1}{2}}^{2} 2^{x} d x-\int_{1}^{2} \ell n x d x$

$\Rightarrow\left[\frac{2^{x}}{\ln 2}\right]_{1 / 2}^{2}-[x \ln x-x]_{1}^{2}$

$\Rightarrow \frac{\left(2^{2}\right)-2^{1 / 2}}{\log _{\mathrm{e}} 2}-(2 \ln 2-1)$

$\Rightarrow \frac{\left(2^{2}-\sqrt{2}\right)}{\log _{\mathrm{e}} 2}-2 \ln 2+1$

$\therefore \alpha=2^{2}-\sqrt{2}, \beta=-2, \gamma=1$

$\Rightarrow(\alpha+\beta+2 \gamma)^{2}$

$\Rightarrow\left(2^{2}-\sqrt{2}-2-2\right)^{2}$

$\Rightarrow(\sqrt{2})^{2}=2$