If the area enclosed between the curves

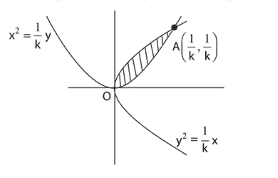
Two curves will intersect in the Ist quadrant at

$A\left(\frac{1}{k}, \frac{1}{k}\right)$

$\because$ area of shaded region $=1 .$

$\therefore \int_{0}^{\frac{1}{k}}\left(\frac{\sqrt{x}}{\sqrt{k}}-k x^{2}\right) d x=1$

$\Rightarrow\left(\frac{1}{\sqrt{k}} \cdot \frac{x^{\frac{3}{2}}}{\frac{3}{2}}\right)_{0}^{\frac{1}{k}}-\left(k \cdot \frac{x^{3}}{3}\right)_{0}^{\frac{1}{k}}=1$

$\Rightarrow \frac{2}{3 \sqrt{k}} \cdot \frac{1}{k^{\frac{3}{2}}}-\frac{k}{3 k^{3}}=1$

$\Rightarrow \frac{2}{3 k^{2}}-\frac{1}{3 k^{2}}=1$

$\Rightarrow 3 k^{2}=1$

$\Rightarrow k=\pm \frac{1}{\sqrt{3}}$

$\therefore \quad k=\frac{1}{\sqrt{3}}$ $(\because k>0)$