If the angle of elevation of a cloud from a point h metres above a lake is a and the angle of depression of its reflection in the lake be b,

Let $C^{\prime}$ be the image of cloud $C$. We have $\angle C A B=\alpha$ and $\angle B A C^{\prime}=\beta$.

Again let  .and  be the distance of cloud from point of observation.

We have to prove that

$A C=\frac{2 h \sec \alpha}{(\tan \beta-\tan \alpha)}$

The corresponding figure is as follows

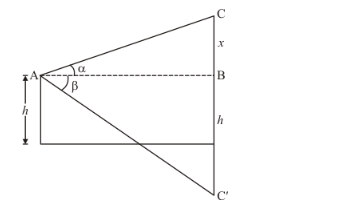
We use trigonometric ratios.

In 

$\Rightarrow \quad \tan \alpha=\frac{B C}{A B}$

$\Rightarrow \quad \tan \alpha=\frac{x}{A B}$

Again in 

$\Rightarrow \quad \tan \beta=\frac{B C^{\prime}}{A B}$

$\Rightarrow \quad \tan \beta=\frac{x+2 h}{A B}$

Now,

$\Rightarrow \tan \beta-\tan \alpha=\frac{x+2 h}{A B}-\frac{x}{A B}$

$\Rightarrow \tan \beta-\tan \alpha=\frac{2 h}{A B}$

$\Rightarrow \quad A B=\frac{2 h}{\tan \beta-\tan \alpha}$

Again in $\triangle A B C$

$\Rightarrow \quad \cos \alpha=\frac{A B}{A C}$

$\Rightarrow \quad A C=\frac{A B}{\cos \alpha}$

$\Rightarrow \quad A C=\frac{2 h \sec \alpha}{(\tan \beta-\tan \alpha)}$

Hence distance of cloud from points of observation is $\frac{2 h \sec \alpha}{\tan \beta-\tan \alpha}$