Question:
If $\tan \theta=\frac{3}{4}$, find the value of $\frac{1-\cos \theta}{1+\cos \theta}$.
Solution:
Given: $\tan \theta=\frac{3}{4}$
We have to find the value of the expression $\frac{1-\cos \theta}{1+\cos \theta}$.
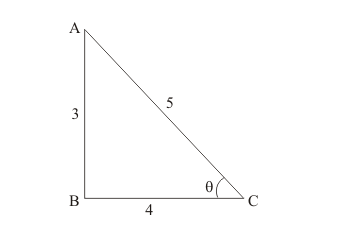
From the above figure, we have
$A C=\sqrt{A B^{2}+B C^{2}}$
$=\sqrt{3^{2}+4^{2}}$
$=5$
$\Rightarrow \cos \theta=\frac{4}{5}$
Therefore,
$\frac{1-\cos \theta}{1+\cos \theta}=\frac{1-\frac{4}{5}}{1+\frac{4}{5}}$
$=\frac{1}{9}$
Hence, the value of the given expression is $\frac{1}{9}$.
