If sin (A−B)=12 and cos (A+B)=12, 0° <A+B≥90°, A<B find A and B.

Given:

$\sin (A-B)=\frac{1}{2} \ldots \ldots$(1)

$\cos (A+B)=\frac{1}{2}$....(2)

We know that,

$\sin 30^{\circ}=\frac{1}{2}$....(3)

$\cos 60^{\circ}=\frac{1}{2}$....(4)

Now by comparing equation (1) and (3)

We get,

$A-B=30$......(5)

Now by comparing equation (2) and (4)

We get,

$A+B=60 \ldots(6)$

Now to get the values of A and B, let us solve equation (5) and (6) simultaneously

Therefore by adding equation (5) and (6)

We get,

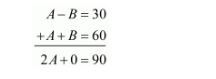
Therefore,

$2 A=90$

$\Rightarrow A=\frac{90}{2}$

$\Rightarrow A=45^{\circ}$

Hence $A=45^{\circ}$

Now by subtracting equation (5) from equation (6)

We get,

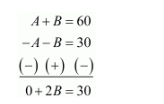
Therefore,

$2 B=30$

$\Rightarrow B=\frac{30}{2}$

$\Rightarrow B=15^{\circ}$

Hence $B=15^{\circ}$

Therefore the values of A and B are as follows

$A=45^{\circ}$ and $B=15^{\circ}$