If radii of the two concentric circles are 15 cm and 17 cm,

We are given that radii of two concentric circles are 15 cm and 17 cm

We have to find the length of each chord of one circle which is tangent to other

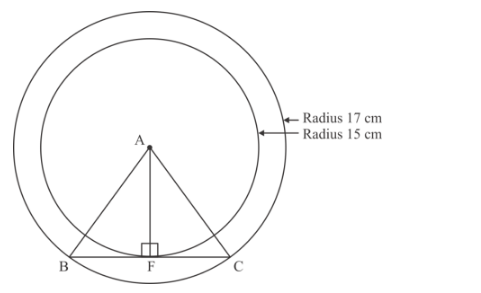
Let A be the centre of the two concentric circles

Let BC be the chord of bigger circle tangent to smaller at F

Therefore AF is the radius of smaller circle

AB is the radius of bigger circle

We know that radius of a circle is perpendicular to its tangent

Therefore $A F \perp B C$

$\triangle A F B$

$\angle A F B=90^{\circ}$

Therefore

$B F=\sqrt{A B^{2}-A F^{2}}$ [Using Pythagoras theorem]

$=\sqrt{(17)^{2}-(15)^{2}} \mathrm{~cm}$

$=\sqrt{289-225} \mathrm{~cm}$

$=\sqrt{64} \mathrm{~cm}$

$=8 \mathrm{~cm}$

We know that a perpendicular from centre of circle to chord of circle bisects the chord

Therefore BF = FC = 8 cm

Length of chord $=B F+F C$

$=8+8$

$=16 \mathrm{~cm}$

Hence option (b) is correct.