If Q.No. 14, c =

Solution:

We have to find the value of c

Given $f(x)=a x^{3}+b x-c$ is divisible by the polynomial $g(x)=x^{2}+b x+c$

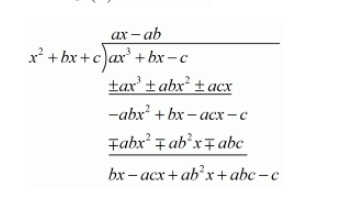
We must have

$b x-a c x+a b^{2} x+a b c-c=0$ for all $x$

$x\left(b-a c+a b^{2}\right)+c(a b-1)=0$ …… (1)

$c(a b-1)=0$

Since $c \neq 0$, so

$a b-1=0$

$a b=1$

Now in the equation (1) the condition is true for all x. So put x = 1 and also we have ab = 1

Therefore we have

$b-a c+a b^{2}=0$

$b+a b^{2}-a c=0$

$b(1+a b)-a c=0$

Substituting $a=\frac{1}{b}$ and $a b=1$ we get,

$b(1+1)-\frac{1}{b} \times c=0$

$2 b-\frac{1}{b} \times c=0$

$-\frac{1}{b} \times c=-2 b$

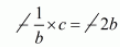
$c=2 b \times \frac{b}{1}$

$c=2 b^{2}$

Hence, the correct alternative is (c)