If Q is a point oh the side SR of a ΔPSR such that PQ = PR, then prove that PS > PQ.
Thinking Process
Use the property of a triangle that if two sides are equal then their opposite angles are also equal. Also use the property that side opposite to greater
angle is longer.
Given in $\triangle P S R, Q$ is a point on the side $S R$ such that $P Q=P R$.
To prove $P S>P Q$
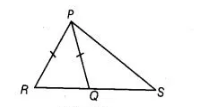
Proof $\ln \Delta P R Q$, $P Q=P R$ [given]
$\Rightarrow$ $\angle R=\angle P Q R$ ...(i)
[angles opposite to equal sides are equal]
But $\angle P Q R>\angle S$ ...(ii)
[exterior angle of a triangle is greater than each of the opposite interior angle]
From Eqs. (i) and (ii), $\angle R>\angle S$
$\Rightarrow \quad P S>P R$ [side opposite to greater angle is longer]
$\Rightarrow$ $P S>P Q$ $[\because P Q=P R]$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.