Question:
If $\mathrm{Q}(0,-1,-3)$ is the image of the point $\mathrm{P}$ in the plane $3 x-y+4 z=2$ and $R$ is the point $(3,-1,-2)$, then the area (in sq. units) of $\triangle \mathrm{PQR}$
Correct Option: , 4
Solution:
$\mathrm{R}$ lies on the plane.
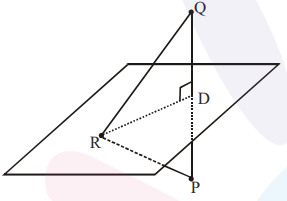
$\mathrm{DQ}=\frac{|1-12-2|}{\sqrt{9+1+16}}=\frac{13}{\sqrt{26}}=\sqrt{\frac{13}{2}}$
$\Rightarrow P Q=\sqrt{26}$
Now, $\mathrm{RQ}=\sqrt{9+1}=\sqrt{10}$
$\Rightarrow \mathrm{RD}=\sqrt{10-\frac{13}{2}}=\sqrt{\frac{7}{2}}$
Hence, $\operatorname{ar}(\triangle \mathrm{PQR})=\frac{1}{2} \times \sqrt{26} \times \sqrt{\frac{7}{2}}=\frac{\sqrt{91}}{2}$.
