Question:
If PT is a tangent to a circle with centre O and PQ is a chord of the circle such that ∠QPT = 70∘ then find the measure of ∠POQ
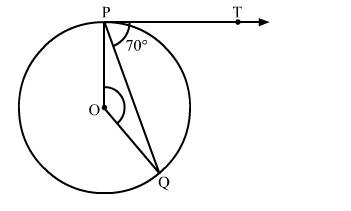
Solution:
We know that the radius and tangent are perperpendular at their point of contact.
∴∠OPT = 90∘
Now, ∠OPQ = ∠OPT − ∠TPQ = 90∘ − 70∘ = 20∘
Since, OP = OQ as both are radius
∴∠OPQ = ∠OQP = 20∘ (Angles opposite to equal sides are equal)
Now, In isosceles △POQ
∠POQ + ∠OPQ + ∠OQP = 180∘ (Angle sum property of a triangle)
⇒ ∠POQ = 180∘ − 20∘ − 20∘ = 140∘
