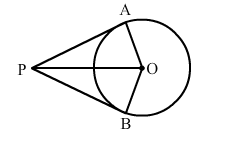
If PA and PB are two tangents to a circle with centre O, such that ∠APB = 80°, then ∠AOP = ?

(b) 50°

Given, $P A$ and $P B$ are two tangents to a circle with centre $O$ and $\angle A P B=80^{\circ}$.

$\therefore \angle A P O=\frac{1}{2} \angle A P B=40^{\circ}$

[ $S$ ince they are equally inclined to the line segment joining the centre to that point]

and $\angle O A P=90^{\circ}$

[S ince tangents drawn from an external point are perpendicular to the radius at the point of contact]

Now, in triangle $A O P:$

$\angle A O P+\angle O A P+\angle A P O=180^{\circ}$

$\Rightarrow \angle A O P+90^{\circ}+40^{\circ}=180^{\circ}$

$\Rightarrow \angle A O P=180^{\circ}-130^{\circ}$

$\Rightarrow \angle A O P=50^{0}$