If one of the zeroes of the cubic polynomial

(a) Let p(x) = x3 + ax2 + bx + c

Let a, p and y be the zeroes of the given cubic polynomial p(x).

∴                                                      α = -1                                                              [given]

and         p(−1) = 0

⇒           (-1)3 + a(-1)2 + b(-1) + c = 0

⇒                             -1 + a- b + c = 0

⇒                                                  c = 1 -a + b                                                             …(i)

We know that,

Product of all zeroes $=(-1)^{3} \cdot \frac{\text { Constant term }}{\text { Coefficient of } x^{3}}=-\frac{c}{1}$

$\alpha \beta y=-c$

⇒                         (-1)βγ = −c                                                                             [∴α = -1]

⇒                            βγ = c

⇒                           βγ = 1 -a + b                                                                [from Eq. (i)]

Hence, product of the other two roots is 1 -a + b.

Alternate Method

Since, -1 is one of the zeroes of the cubic polynomial f(x) = x2 + ax2 + bx + c i.e., (x + 1) is a factor of f{x).

Now, using division algorithm,

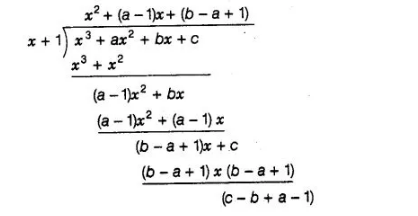
⇒x3 + ax2 + bx +c = (x + 1) x {x2 + (a – 1)x + (b – a + 1)> + (c – b + a -1)

⇒x3 + ax2 + bx + (b – a + 1) = (x + 1) {x2 + (a – 1)x + (b -a+ 1}}

Let a and p be the other two zeroes of the given polynomial, then

Product of zeroes $=(-1) \alpha \cdot \beta=\frac{-\text { Constant term }}{\text { Coefficient of } x^{3}}$

$\Rightarrow \quad-\alpha \cdot \beta=\frac{-(b-a+1)}{1}$

$\Rightarrow \quad \alpha \beta=-a+b+1$

Hence, the required product of other two roots is $(-a+b+1)$.