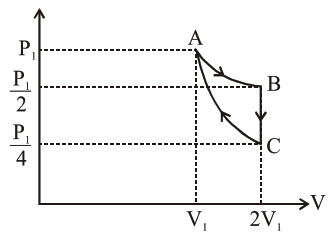
If one mole of an ideal gas at $\left(\mathrm{P}_{1}, \mathrm{~V}_{1}\right)$ is allowed to expand reversibly and isothermally (A to B) its pressure is reduced to one-half of the original pressure (see figure). This is followed by a constant volume cooling till its pressure is reduced to one-fourth of the initial value $(B \rightarrow C)$. Then it is restored to its initial state by a reversible adiabatic compression (C to A). The net workdone by the gas is equal to :
Correct Option: 1
$A-B=$ isothermal process
$\mathrm{W}_{\mathrm{AB}}=\mathrm{P}_{1} \mathrm{~V}_{1} \ln \left[\frac{2 \mathrm{~V}_{1}}{\mathrm{~V}_{1}}\right]=\mathrm{P}_{1} \mathrm{~V}_{1} \ln (2)$
$\mathrm{B}-\mathrm{C} \rightarrow$ Isochoric process
$\mathrm{W}_{\mathrm{BC}}=0$
$\mathrm{C}-\mathrm{A} \rightarrow$ Adiabatic process
$\mathrm{W}_{\mathrm{CA}}=\frac{\mathrm{P}_{1} \mathrm{~V}_{1}-\frac{\mathrm{P}_{1}}{4} \times 2 \mathrm{~V}_{1}}{1-\gamma}=\frac{\mathrm{P}_{1} \mathrm{~V}_{1}\left[1-\frac{1}{2}\right]}{1-\gamma}=\frac{\mathrm{P}_{1} \mathrm{~V}_{1}}{2(1-\gamma)}$
$\mathrm{W}_{\text {net }}=\mathrm{W}_{\mathrm{AB}}+\mathrm{W}_{\mathrm{BC}}+\mathrm{W}_{\mathrm{CA}} \quad\left\{\mathrm{P}_{1} \mathrm{~V}_{1}=\mathrm{RT}\right\}$
$=\mathrm{P}_{1} \mathrm{~V}_{1} \ln (2)+0+\frac{\mathrm{P}_{1} \mathrm{~V}_{1}}{2(1-\gamma)}$
$\mathrm{W}_{\text {net }}=\mathrm{RT}\left[\ln (2)-\frac{1}{2(\gamma-1)}\right]$
Option (1) is correct.
