If $\mathrm{n}$ is the number of solutions of the equation $2 \cos x\left(4 \sin \left(\frac{\pi}{4}+x\right) \sin \left(\frac{\pi}{4}-x\right)-1\right)=1, x \in[0, \pi]$ and $S$ is the sum of all these solutions, then the ordered pair $(\mathrm{n}, \mathrm{S})$ is :
Correct Option: 1
$2 \cos x\left(4 \sin \left(\frac{\pi}{4}+x\right) \sin \left(\frac{\pi}{4}-x\right)-1\right)=1$
$2 \cos x\left(4\left(\sin ^{2} \frac{\pi}{4}-\sin ^{2} x\right)-1\right)=1$
$2 \cos x\left(4\left(\frac{1}{2}-\sin ^{2} x\right)-1\right)=1$
$2 \cos x\left(2-4 \sin ^{2} x-1\right)=1$
$2 \cos x\left(1-4 \sin ^{2} x\right)=1$
$4 \cos ^{3} x-3 \cos x=\frac{1}{2}$
$\cos 3 x=\frac{1}{2}$
$\mathrm{X} \in[0, \pi] \therefore 3 \mathrm{x} \in[0,3 \pi]$
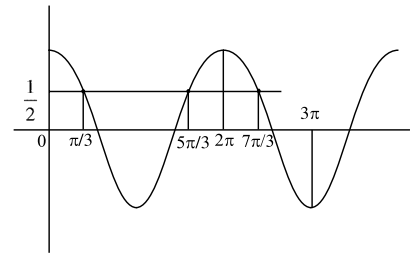
$2 \cos x\left(4 \cos ^{2} x-3\right)=1$
