If n is the number of irrational terms in the expansion of

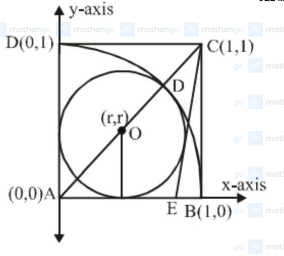
Here $\mathrm{AO}+\mathrm{OD}-1$ or $(\sqrt{2}+1) \mathrm{r}=1$

$\Rightarrow \quad \mathbf{r}=\sqrt{2-1}$

equation of circle $(x-r)^{2}+(y-r)^{2}=r^{2}$

Equation of CE

$y-1-m(x-1)$

$m x-y+1-M=0$

It is tangent to circle

$\therefore \quad\left|\frac{m r-r+1-m}{\sqrt{m^{2}+1}}\right|=r$

$\left|\frac{(m-1) r+1-m}{\sqrt{m^{2}+1}}\right|=r$

$\frac{(m-1)^{2}(r-1)^{2}}{m^{2}+1}=r^{2}$

Put $\mathrm{r}=\sqrt{2}-1$

On solving $\mathrm{m}-2-\sqrt{3}, 2+\sqrt{3}$