If in a triangle $\mathrm{ABC}, \mathrm{AB}=5$ units, $\angle \mathrm{B}=\cos ^{-1}\left(\frac{3}{5}\right)$ and radius of circumcircle of $\triangle \mathrm{ABC}$ is 5 units, then the area (in sq. units) of $\triangle \mathrm{ABC}$ is :
Correct Option: , 3
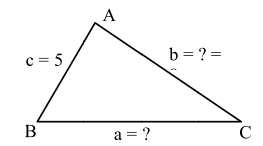
As, $\operatorname{cosB}=\frac{3}{5} \Rightarrow \mathrm{B}=53^{\circ}$
As, $R=5 \Rightarrow \frac{c}{\sin c}=2 R$
$\Rightarrow \frac{5}{10}=\sin \mathrm{c} \Rightarrow \mathrm{C}=30^{\circ}$
Now, $\frac{\mathrm{b}}{\sin \mathrm{B}}=2 \mathrm{R} \Rightarrow \mathrm{b}=2(5)\left(\frac{4}{5}\right)=8$
Now, by cosine formula
$\cos \mathrm{B}=\frac{\mathrm{a}^{2}+\mathrm{c}^{2}-\mathrm{b}^{2}}{2 \mathrm{ac}}$
$\Rightarrow \frac{3}{5}=\frac{a^{2}+25-64}{2(5) a}$
$\Rightarrow a^{2}-6 a-3 g=0$
$\therefore \mathrm{a}=\frac{6 \pm \sqrt{192}}{2}=\frac{6 \pm 8 \sqrt{3}}{2}$
$\Rightarrow 3+4 \sqrt{3}($ Reject $a=3-4 \sqrt{3})$
Now, $\Delta=\frac{\mathrm{abc}}{4 \mathrm{R}}=\frac{(3+4 \sqrt{3})(8)(5)}{4(5)}=2(3+4 \sqrt{3})$
$\Rightarrow \Delta=(6+8 \sqrt{3})$
$\Rightarrow$ Option (3) is correct.
