If f : A → A, g : A → A are two bijections, then prove that

Given: $A \rightarrow A, g: A \rightarrow A$ are two bijections.

Then, fog: $A \rightarrow A$

(i) Injectivity of fog:
Let x and y be two elements of the domain (A), such that

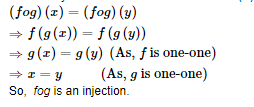
(ii) Surjectivity of fog:
Let z be an element in the co-domain of fog (A).

Now, $z \in A$ (co-domain of $f$ ) and $f$ is a surjection.

So, $z=f(y)$, where $y \in A$ (domain of $f$ ) ... (1)

Now, $y \in A$ (co-domain of $g$ ) and $g$ is a surjection.

So, $y=g(x)$, where $x \in A$ (domain of $g$ ) ...(2)

From (1) and (2),

$z=f(y)=f(g(x))=(f o g)(x)$, where $x \in A$ (domain of $f o g$ )

So, fog is a surjection.