If D is a point on the side BC of a ΔABC such that AD bisects ∠BAC. Then,
(a) BD = CD
(b) BA > BD
(c) BD > BA
(d)CD > CA
Thinking Process
(i) Firstly, use the property, exterior angle of a triangle is greater than interior opposite
angle.
(ii) Secondly, use the property that in a triangle, the side opposite to the greater angle is longer.
(b) Given, $\triangle A B C$ such that $A D$ bisects $\angle B A C$
$\therefore$ $\angle B A D=\angle C A D$ $\ldots(i)$
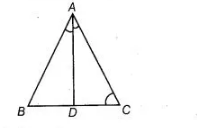
In $\triangle A C D, \angle B D A$ is an exterior angle.
$\therefore \quad \angle B D A>\angle C A D$ $\ldots(i)$
$[\because$ exterior angle $>$ interior opposite angle]
$\Rightarrow \quad \angle B D A>\angle B A D \quad$ [from Eq. (i)]
$\Rightarrow$ $B A>B D$ [side opposite to greater angle is greater]
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.