If D, E and F are respectively the midpoints of sides AB, BC and CA of

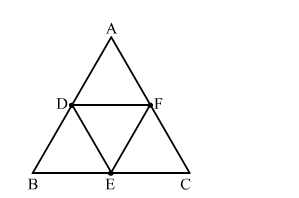
By using mid theorem i.e., the segment joining two sides of a triangle at the midpoints of those sides is parallel to the third side and is half the length of the third side.

$\therefore \mathrm{DF} \| \mathrm{BC}$

and

$\mathrm{DF}=\frac{1}{2} \mathrm{BC}$

$\Rightarrow \mathrm{DF}=\mathrm{BE}$

Since, the opposite sides of the quadrilateral are parallel and equal.
Hence, BDFE is a parallelogram
Similarly, DFCE is a parallelogram.
Now, In △ABC and △EFD
∠ABC = ∠EFD         (Opposite angles of a parallelogram)
∠BCA = ∠EDF       (Opposite angles of a parallelogram)
By AA similarity criterion, △ABC ∼ △EFD
If two triangles are similar, then the ratio of their areas is equal to the ratio of the squares of their corresponding sides.

$\therefore \frac{\operatorname{area}(\triangle \mathrm{DEF})}{\operatorname{area}(\triangle \mathrm{ABC})}=\left(\frac{\mathrm{DF}}{\mathrm{BC}}\right)^{2}=\left(\frac{\mathrm{DF}}{2 \mathrm{DF}}\right)^{2}=\frac{1}{4}$

Hence, the ratio of the areas of △DEF and △ABC is 1 : 4.