Question:
If BM and CN are the perpendiculars drawn on the sides AC and AB of the ΔABC, prove that the points B, C, M and N are concyclic.
Solution:
Given In ΔABC, BM ⊥ AC and CN ⊥ AB.
To prove Points B, C, M and N are con-cyclic.
Construction Draw a circle passing through the points B, C, M and N.
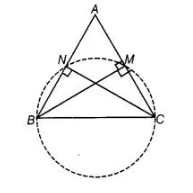
Proof Suppose, we consider SC as a diameter of the circle. Also, we know that SC subtends a 90° to the circle.
So, the points M and N should be on a circle.
Hence, BCMN form a con-cyclic quadrilateral. Hence proved.
