If bisectors of opposite angles of a cyclic quadrilateral ABCD intersect the circle, circumscribing it at the points P and Q, prove that PQ is a
diameter of the circle.
Thinking Process
Use the property of cyclic quardrilateral, the sum of opposite angles of cyclic quadrilateral is supplementary. Further, simplify it to prove the required
result.
Given, ABCD is a cyclic quadrilateral.
DP and QB are the bisectors of ∠D and ∠B, respectively.
To prove PQ is the diameter of a circle.
Construction Join QD and QC.
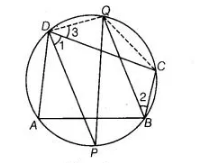
Proof Since, $A B C D$ is a cyclic quadrilateral.
$\therefore \quad \angle C D A+\angle C B A=180^{\circ}$
[sum of opposite angles of cyclic quadrilateral is $180^{\circ}$ ]
On dividing both sides by 2 , we get
$\frac{1}{2} \angle C D A+\frac{1}{2} \angle C B A=\frac{1}{2} \times 180^{\circ}=90^{\circ}$
$\Rightarrow$ $\angle 1+\angle 2=90^{\circ}$ ....(i)
$\left[\angle 1=\frac{1}{2} \angle C D A\right.$ and $\left.\angle 2=\frac{1}{2} \angle C B A\right]$
But $\angle 2=\angle 3$ [angles in the same segment $Q C$ are equal] ... (ii)
$\angle 1+\angle 3=90^{\circ}$
From Eqs. (i) and (ii), $\angle P D Q=90^{\circ}$
Hence, $P Q$ is a diameter of a circle, because diameter of the circle. Subtends a right angle at the circumference.
