If bisectors of ∠A and ∠B of a quadrilateral ABCD intersect each other at P, of ∠B and ∠C at Q,

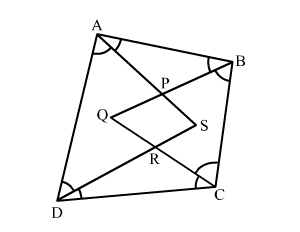
Given: In quadrilateral ABCD, AS, BQ, CQ and DS are angle bisectors of angles A, B, C and D, respectively.

∠QPS = ∠APB        (Vertically opposite angles)          ...(1)

In Δ∆APB,

∠APB + ∠PAB + ∠ABP = 180°        (Angle sum property of triangle.)

$\Rightarrow \angle A P B+\frac{1}{2} \angle A+\frac{1}{2} \angle B=180^{\circ}$

$\Rightarrow \angle A P B=180^{\circ}-\frac{1}{2}(\angle A+\angle B)$             ...(2)

From (1) and (2), we get

$\angle Q P S=180^{\circ}-\frac{1}{2}(\angle A+\angle B)$             ...(3)

Similarly, $\angle Q R S=180^{\circ}-\frac{1}{2}(\angle C+\angle D)$         ...(4)

From (3) and (4), we get

$\angle Q P S+\angle Q R S=360^{\circ}-\frac{1}{2}(\angle A+\angle B+\angle C+\angle D)$

$=360^{\circ}-\frac{1}{2}\left(360^{\circ}\right)$

$=360^{\circ}-180^{\circ}$

$=180^{\circ}$

So, PQRS is a quadrilateral whose opposite angles are supplementary.

Hence, the correct option is (d).