If at some time of the day the ratio of the height of a vertically standing pole to the length of its shadow on the ground is

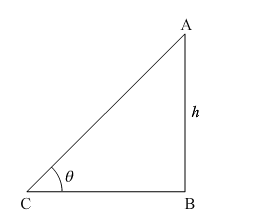
Let AB be the vertically standing pole of height h units and CB be the length of its shadow of s units.

Since, the ratio of length of pole and its shadow at some time of day is given to be $\sqrt{3}: 1$.

$\Rightarrow \frac{\mathrm{AB}}{\mathrm{BC}}=\frac{\sqrt{3}}{1}$

$\therefore \ln \triangle \mathrm{ABC}:$

$\tan (\theta)=\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{\sqrt{3}}{1}=\sqrt{3}$

$\Rightarrow \tan (\theta)=\tan 60^{\circ}$

$\Rightarrow \theta=60^{\circ}$