If APB and CQD are two parallel lines,

(c) Given, $A P B$ and $C Q D$ are two parallel lines.

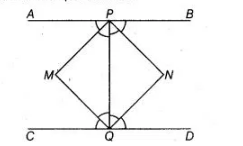
Let the bisectors of angles $A P Q$ and $C Q P$ meet at a point $M$ and bisectors of angles $B P Q$ and $P Q D$ meet at a point $N$.

Join $P M, M Q, Q N$ and $N P$.

Since, $A P B \| C Q D$

Then, $\quad \angle A P Q=\angle P Q D \quad$ [alternate interior angles]

$\Rightarrow \quad \angle M P Q=2 \angle N Q P$

[since, $P M$ and $N Q$ are the angle bisectors of $\angle A P Q$ and $\angle D Q P$ respectively]

$\Rightarrow \quad \angle M P Q=\angle N Q P \quad$ [dividing both sides by 2]

[since, alternate interior angles are equal.]

$\therefore$ $P M \| Q N$

Similarly, $\angle B P Q=\angle C Q P$ [alternate interior angles]

$\therefore$ $P N \| Q M$

So, quadrilateral $P M Q N$ is a parallelogram.

$\because$ $\angle C Q D=180^{\circ}$  [since, $C Q D$ is a line]

$\Rightarrow$ $\angle C Q P+\angle D Q P=180^{\circ}$

$\Rightarrow \quad 2 \angle M Q P+2 \angle N Q P=180^{\circ}$

[since, $M Q$ and $N Q$ are the bisectors of the angles $C Q P$ and $D Q P$ ]

$\Rightarrow \quad 2(\angle M Q P+\angle N Q P)=180^{\circ}$

$\Rightarrow \quad \angle M Q N=90^{\circ}$

Hence, PMQN is a rectangle.