If Δ ABC is isosceles with AB = AC and C (O, r) is

Solution:

Let us first put the given data in the form of a diagram.

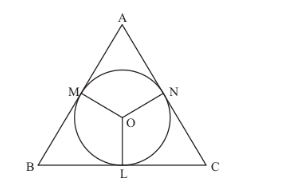
It is given that triangle ABC is isosceles with

AB = AC …… (1)

By looking at the figure we can rewrite the above equation as,

AM + MB = AN + NC

From the property of tangents we know that the length of two tangents drawn to a circle from the same external point will be equal. Therefore,

AM = AN

Let us substitute AN with AM in the equation (1). We get,

AM + MB = AM + NC

MB = NC …… (2)

From the property of tangents we know that the length of two tangents drawn from the same external point will be equal. Therefore we have,

MB = BL

NC = LC

But from equation (2), we have found that

MB = NC

Therefore,

BL = LC

Thus we have proved that point L bisects side BC.