Question:
If ABC is an equilateral triangle inscribed in a circle and P be any point on the minor arc BC which does not coincide with B or C, then prove that PA is angle bisector of ∠BPC.
Solution:
Given ΔABC is an equilateral triangle inscribed in a circle and P be any point on the minor arc BC which does not coincide with B or C.
To prove PA is an angle bisector of ∠BPC.
Construction Join PB and PC.
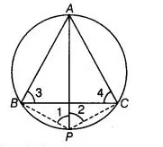
Proof Since, $\triangle A B C$ is an equilateral triangle.
$\angle 3=\angle 4=60^{\circ}$
Now, $\angle 1=\angle 4=60^{\circ}$ .....(i)
[angles in the same segment $A B$ ]
$\angle 2=\angle 3=60^{\circ}$ $\ldots$ (ii)
[angles in the same segment $A C$ ]
$\therefore$ $\angle 1=\angle 2=60^{\circ}$
Hence, $P A$ is the bisector of $\angle B P C$.
Hence proved.
