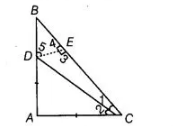
Question:
If ABC is a right angled triangle such that AB = AC and bisector of angle C intersects the side AB at D, then prove that AC + AD = BC.
Solution:
Given in right angled $\triangle A B C, A B=A C$ and $C D$ is the bisector of $\angle C$. Construction Draw $D E \perp B C$.
To prove $A C+A D=B C$
Proof In right angled $\triangle A B C, A B=A C$ and $B C$ is a hypotenuse
[given]
$\therefore \quad \angle A=90^{\circ}$
In $\triangle D A C$ and $\triangle D E C$, $\angle A=\angle 3=90^{\circ}$